Question

Plot four points on that graph, the leftmost point and three additional points

Answer 1

Given the function:

`f(x)=\sqrt[]{x+4}`

This function is a radical function. The domain of this function comprehends any value of x for which the radicand is not negative.

The leftmost point of the function is determined by the value of x for which the radicand is zero.

To determine this value of x, you have to equal the radicand to zero and solve:

`\begin{gathered} x+4=0 \\ x+4-4=0-4 \\ x=-4 \end{gathered}`

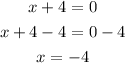
For x=-4 the radicand is equal to zero and the function is also equal to zero, so the coordinates for the leftmost point are:

`(-4,0)`

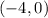
For the next three points, you have to choose 3 positive values of x, replace them into the formula and solve for f(x).

I will use 0, 5, and 12

For x=0

`\begin{gathered} f(x)=\sqrt[]{x+4} \\ f(0)=\sqrt[]{0+4} \\ f(0)=\sqrt[]{4} \\ f(0)=2 \end{gathered}`

The coordinates are:

`(0,2)`

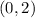
For x= 5

`\begin{gathered} f(x)=\sqrt[]{x+4} \\ f(5)=\sqrt[]{5+4} \\ f(5)=\sqrt[]{9} \\ f(5)=3 \end{gathered}`

The coordinates are:

`(5,3)`

For x= 12

`\begin{gathered} f(x)=\sqrt[]{x+4} \\ f(12)=\sqrt[]{12+4} \\ f(12)=\sqrt[]{16} \\ f(12)=4 \end{gathered}`

The coordinates are

`(12,4)`

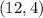
Once you have determined the coordinates of the four points, plot them and graph the function: