Question

Find the value of two integers if their sum is one hundred and seventy one and their difference is twenty-five.write the value of the greater integer

Answer 1

Let x be the greater integer

Let y be the smaller integer

their sum is one hundred and seventy one:

`x+y=171`

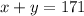
their difference is twenty-five:

`x-y=25`

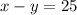
Use the next system of equations:

`\begin{gathered} x+y=171 \\ x-y=25 \end{gathered}`

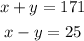
1. Solve y in the second equation:

`\begin{gathered} x-y=25 \\ -y=25-x \\ y=-25+x \end{gathered}`

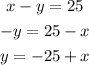
2. Substitute the y in the first equation by th value you get in step 1:

`x+(-25+x)=171`

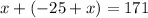
3. Solve x:

`\begin{gathered} x-25+x=171 \\ 2x-25=171 \\ 2x=171+25 \\ 2x=196 \\ x=(196)/(2) \\ \\ x=98 \end{gathered}`

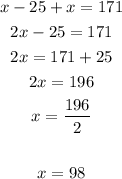
Then, the greater integer is 98