Question

in the figure below, two chords intersect inside the circle at point V. suppose that VN = 22.5, VJ = 9, and VM = 18. Find JK.

Answer 1

To solve this problem we have to use the intersecting chords theorem which states a proportion between the four resulting segments,

Based on this theorem, we can define the following proportion

`VM* VN=KV* VJ`

First, we find VK. We have to replace the given information

`\begin{gathered} 18*22.5=KV*9 \\ KV=(405)/(9)=45 \end{gathered}`

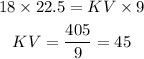
Now, by the sum of segments, we define an equation for JK.

`\begin{gathered} JK=VJ+KV \\ JK=9+45=54 \end{gathered}`

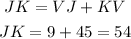
Therefore, the chord JK is 54 units long.