Question

Graph each quadratic function. State the domain and range. Also include a chart.

Answer 1

We can construct a chart, a table for the values of the given function as follows:

1. We need to have the function g(x) = -4x^2.

2. We can obtain the values for the function for the values:

x = -4, x = -2, x = 0, x = 2, x = 4.

3. We need to evaluate the function for each of these values.

4. Finally, we can have a table of the values of x and y.

Having this information into account, we can proceed as follows:

1. x = -4

`f(-4)=-4(-4)^2=-4\cdot(16)=-64\Rightarrow f(-4)=-64`

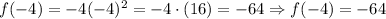
2. x = -2

`f(-2)=-4(-2)^2=-4(4)\Rightarrow f(-2)=-16`

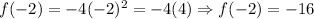
3. x = 0

`f(0)=-4(0)^2=-4\cdot0\Rightarrow f(0)=0`

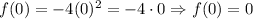
4. x = 2

`f(2)=-4(2)^2=-4\cdot4\Rightarrow f(2)=-16`

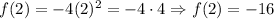
5. x = 4

`f(4)=-4(4)^2=-4\cdot16\Rightarrow f(4)=-64`

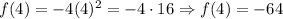
Then, having these values, we can construct the values for the function using these values:

We can draw part of this function using these values. We have to remember that, in functions, we can say that y = f(x).

We can also say that the domain of the function is, in interval notation:

`(-\infty,\infty)`

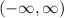
And the range, as we can see from the values, is as follows (using interval notation):

`(-\infty,0\rbrack`

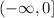
This is because the values for y (or f(x)) are less or equal to zero.

In summary, we can have a table to construct a graph using the values for the independent variable and plug these values in the function to obtain the values for y.

We need to remember that y = f(x). Additionally, this function has a domain from -infinity to infinity (all the values in the Real set), and a range for values from -infinity to 0 (including zero).

A graph for this function is as follows: