D
Step-by-step explanation
the slope of a line is given by
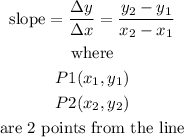
Step 1
find the slope of the table
Let
P1(0,3)
P2(2,-2)
replace
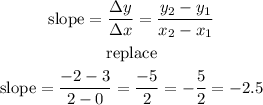
Step 2
find the slope of the line A)
let
P1(-1,3)
P2(-2,1)
replace and calculate
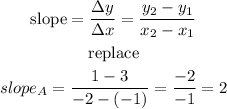
Step 3
find the slope of function at B)
we have the equation in slope-intercept form
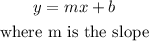
so
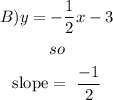
and
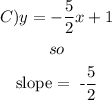
Step 4
finally, the slope of the line graphed at D)
Let
P1(1,-5)
P2(0,1))
replace

so, we can conclude

so, the function that has a lesser slopes than the one in the graph is
(D) -6
therefore, the answer is
D
I hope this helps you