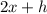We are given the following function:
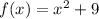
We are asked to determine the following quotient:
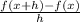
To do that, we will first determine the function f(x + h), to do that we will replace the variable "x" for the variable "x + h", like this:
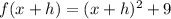
Solving the parenthesis, using the following property:
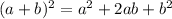
Applying the property:
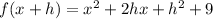
Substituting in the quotient:
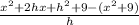
Now we change the sing to the terms inside the parenthesis since it is preceded by a minus sing:
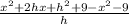
Adding line terms:
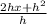
Now we take "h" as a common factor in the numerator:
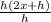
Canceling out the "h":