Question

If x = 12, which equation is true?A-27 + 2x = 51B5(x + 7) = 45C 3(25) - x = 39D 3(25 - x) = 39

Answer 1

To determine which equation is true, let's replace "x" with "12" in each equation and solve.

Let's start with Option A.

`\begin{gathered} -27+2(12)=51 \\ -27+24=51 \\ -3\\e51 \end{gathered}`

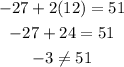
For Option A, at x = 12, the value is not equal to 51 hence, Equation A is not true.

For Option B:

`\begin{gathered} 5(x+7)=45 \\ 5(12+7)=45 \\ 5(19)=45 \\ 95\\e45 \\ \end{gathered}`

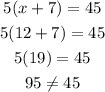
As we can see, Option B is not also true.

Let's check Option C.

`\begin{gathered} 3(25)-x=39 \\ 3(25)-12=39 \\ 75-12=39 \\ 63\\e39 \end{gathered}`

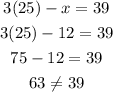
Option C is also not true.

Let's check Option D.

`\begin{gathered} 3(25-x)=39 \\ 3(25-12)=39 \\ 3(13)=39 \\ 39=39 \end{gathered}`

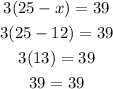
As we can see, at x = 12, Equation D is equal to 39. Hence, Equation D is true.