A regular triangular pyramid has equilateral triangles.
The lateral area (Al) of a triangular pyramid is:
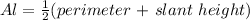
The surface area (As) of a triangular pyramid is:

Step 01: Find Al.
Perimeter = sum of the sides = 6 + 6 + 6 = 18 cm
Slant height = 13 cm
Step 02: Find As.
To find As, first find "h". h can be found according to the figure below:
So, h can be found using the Pythagorean theorem:
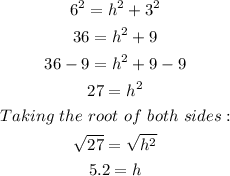
And, find Ab and then find As:
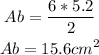
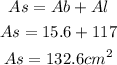
Answer:
Lateral area: 117 cm².
Surface area: 132.6 cm².