The root method requires us to leave the expression that is raised to the power of 2 on one side of the equality. We do so, by applying mathematical operations on both sides of the equation
We begin with the equation
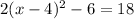
First, we add 6 on both sides, so we get
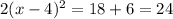
Then, we divide boths sides by 2, so we get
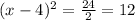
Now, we take the square root on both sides. Have in mind that once we take the square root we should consider the positive and negative root. So we get
![x-4=\pm\sqrt[]{12}](https://img.qammunity.org/2023/formulas/mathematics/college/bc4zjthu4zjwfn6ufdbji0yl6tawpqzltp.png)
Finally, we add 4 on both sides, so we get
![x=4\pm\sqrt[]{12}](https://img.qammunity.org/2023/formulas/mathematics/college/nsxzagesrzwaepnx89dypxj1fzimioiaiq.png)
This is equivalent to have the solutions
![x=4+\sqrt[]{12}](https://img.qammunity.org/2023/formulas/mathematics/college/dquhz568kmr761s311unwp29f843iahojp.png)
and
![x=4-\sqrt[]{12}](https://img.qammunity.org/2023/formulas/mathematics/college/2vwhqyajg94vs3nwry60x5fvi641gbpuod.png)