Question

How many arrangements can be formed using the letters EPIPHANY?

Answer 1

From the word EPIPHANY, we can see that:

E,I,H,A,N,Y are unique and P repeats twice. Then we would have a permutation with repetition. Let's state some data to solve this problem:

n=8 (number of letters)

Repetitions of the letter E: 2

Then:

`\begin{gathered} P_{}(n;a,b,c\ldots)=(n!)/(a!b!c!\ldots)^{_{}}_{} \\ \Rightarrow P(8,2)=(8!)/(2!)=(8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1)/(2\cdot1)=(40320)/(2)=20160 \\ \\ \end{gathered}`

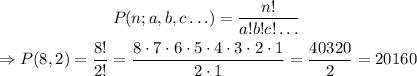
Therefore, we can make 20160 arrangements using the letters EPIPHANY