Question

4) Miguel found a savings account that his late grandmother had opened, but had forgotten about. She haddeposited $4,500 at 2.5% compounded yearly. When Tito checked the balance, there was $22,960.83 in theaccount.How long had the money been in the savings account, gathering interest?

Answer 1

The formula for compound interest would be:

`A=P(1+r)^t`

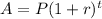
Where

A is the amount accumulated after a time

P is the principal amount deposited

r is the rate of interest (in decimal)

t is the time in years

Given,

P = 4500

r = 2.5%/100 = 0.025

A = 22,960.83

Now, we substitute and solve for t using natural logs. Shown below:

`\begin{gathered} A=P(1+r)^t \\ 22,960.83=4500(1+0.025)^t \\ 22,960.83=4500(1.025)^t \\ 5.1024=1.025^t \end{gathered}`

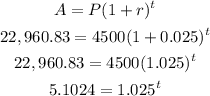
Now, we take natural log (Ln) of both sides and solve for t :

`\begin{gathered} \ln (5.1024)=\ln (1.025^t) \\ \ln (5.1024)=t\ln (1.025) \\ t=(\ln (5.1024))/(\ln (1.025)) \\ t=65.99 \end{gathered}`

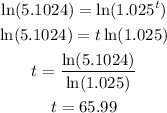
So, the money was approximately 66 years old.