The form of the exponential equation is

a is the initial amount
r is the annual rate in decimal
Since the number of rabbits increases by 250% each year, then
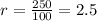
Since the farm started with 12 rabbits, then
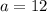
Substitute them in the form of the equation above
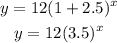
We need to find the time for the rabbits to be 250
Then substitute y by 250 and solve the equation to find x
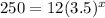
Divide both sides by 12
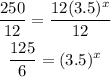
Insert log to both sides
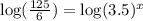
Use the rule of the exponent with log
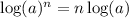
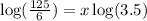
Divide both sides by log(3.5) to find x
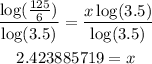
It will take about 2.42 years to be 250 rabbits