Given:
The length of the top diagram is 60 units.
Required:
The length of the bottom diagram.
Step-by-step explanation:
Now the first diagram has two parts 80% and 20%, and the 20% further gives us the second diagram.
So to know the length of second diagram we need to find the 20% of first diagram.
so we need to calculate 20% of 60, that is
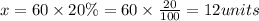
So the length of second diagram is 12 units.
Now the second diagram has two parts 60% and 40%, and the 60% further gives us the third diagram.
So to know the length of third diagram we need to find the 60% of second diagram.
so we need to calculate 60% of 12, that is
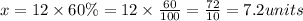
So the length of third diagram is 7.2 units.
Now the third diagram has two parts 30% and 70%, and the 70% further gives us the fourth diagram.
So to know the length of the fourth diagram we need to find the 70% of the third diagram.
So we need to calculate 70% of 7.2, that is
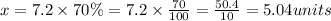
So the length of fourth diagram is 5.04 units
Final Answer:
The length of the bottom diagram, that is the fourth diagram, is 5.04 units.