Answer:
6.55%
Explanation:
Given a random variable X having a normal distribution with:
• Mean, µ = 40
,
• Standard Deviation, σ = 10
We want to find the probability that X is between 55 and 70.
In order to do this, first, we find the z-scores for X=55 and X=70.
The z-score formula is:
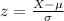
Thus:
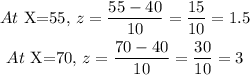
From the z-table:
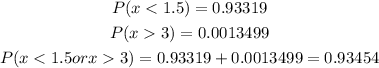
Therefore, using a z-score table, the probability that X assumes a value between 55, 70 is:
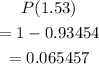
The required probability is 6.55%.