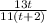Part A: Distance between the 1st and 2nd card at time t.
Distance traveled by 1st car: D1 = 55(t + 2)
Distance traveled by 2nd car: D2 = 65t
The distance between the cars:
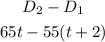
Using the distributive property to remove the parentheses:
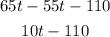
The distance is: 10t - 110.
Part B: Ratio between the distance from the second to the first car.
To find it, do:
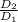
Then,

Dividing numerator and denominator by 5:
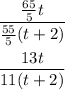
The ratio is:
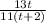
In summary,
The distance is: 10t - 110.
And the ratio is: