Question

Begin by graphing the absolute value function f(x) = lxl. Then use the transformations of this graph to graph the given function:g(x) = |x| + 1 What transformations are needed in order to obtain the graph of g(x) from the graph of f(x)? Select all that apply and then plot the graph. A. Vertical shiftB. Horizontal stretch/shrinkC. Reflection about the y-axis D. Reflection about the x-axis E. Vertical stretch/shrinkF. Horizontal shift

Answer 1

ANSWER and EXPLANATION

We want to transform the graph and find the transformations needed to obtain the graph:

`\begin{gathered} f(x)=|x| \\ g(x)=|x|+1 \end{gathered}`

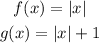
When a function is transformed as follows:

`g(x)\to f(x)+a`

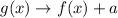
it implies that the function has been shifted vertically upwards by "a" units.

Hence, a transformation of:

`g(x)=|x|+1`

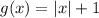
implies that to obtain the graph of g(x), we have to shift the graph of f(x) by 1 unit upwards.

Let us show this on the graph:

Hence, the transformation needed in order to obtain the graph of g(x) from the graph of f(x) is a vertical shift.