Question

Which of the following images (A, B, or C) shows the given figure moving down 2 units and right 3 units? A: (4 , 0) (2, -1)(4, -4)B. (2, -1) (0, -2)(-2, -5) C. (0, 0)(2, -1) (0, -4)

Answer 1

Given:

We get the points A(-3,2), B(-1,1) and C(-3,-2) from the graph.

The transformation of points down 2 units and right 3 units can be written as follows.

`(x,y)\rightarrow(x+3,y-2)`

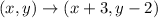
The image of A(-3,2) is

`A(-3,2)\rightarrow(-3+3,2-2)`

`A(-3,2)\rightarrow(0,0)`

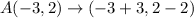
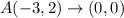
We get the point (0,0).

The image of B(-1,1) is

`B(-1,1)\rightarrow(-1+3,1-2)`

`B(-1,1)\rightarrow(2,-1)`

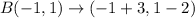
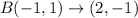
We get the point (2,-1).

The image of C(-3,-2).

`C(-3,-2)\rightarrow(-3+3,-2-2)`

`C(-3,-2)\rightarrow(0,-4)`

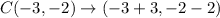
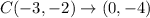
We get the point (0,-4).

Hence the points of the image is

(0,0), (-3,-2) and (0,-4).

Option C is correct.