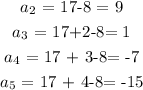Question

Find the four terms of the arithmetic sequence given the first term (a_1=17) and the seventh term (a_7=-31).Given terms:a_1=17 and a_7=-31Find these terms:a_2= Answera_3= Answera_4= Answera_5= Answer

Answer 1

`\begin{gathered} a_2\text{ = 9} \\ a_3\text{ = 1} \\ a_4\text{ = -7} \\ a_5\text{ = -15} \end{gathered}`

Step-by-step explanation:

Here, we want to get find the four terms of the arithmetic sequence from the given terms

The first term is represented by a,

Then each of the next terms is a + (n-1)d

Thus, we have the 7th term as:

`a\text{ + 6d}`

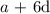
we can get d from here, which is the common difference of terms in the sequence

`\begin{gathered} a\text{ + 6d = -31} \\ 17\text{ +6d = -31} \\ 6d\text{ = =-31-17} \\ 6d\text{ = -48} \\ d\text{ = }(-48)/(6) \\ d\text{ = -8} \end{gathered}`

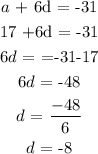
We have the other terms as follows:

`\begin{gathered} a_2\text{ = 17-8 = 9} \\ a_3\text{ = 17+2\lparen-8\rparen = 1} \\ a_4\text{ = 17 + 3\lparen-8\rparen = -7} \\ a_5\text{ = 17 + 4\lparen-8\rparen = -15} \end{gathered}`