Question

Select the values that make the inequality-39 < 51 true. Then write an equivalentinequality, in terms of q.(Numbers written in order from least togreatest going across.)

Answer 1

- The formula for finding the average rate of change is

`\begin{gathered} (\Delta y)/(\Delta x)=(f(x_2)-f(x_1))/(x_2-x_1) \\ \\ where, \\ (x_1,f(x_1)),\text{ and }(x_2,f(x_2))\text{ are the points on the graph} \end{gathered}`

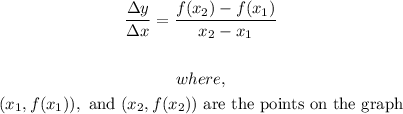
- We have been asked to find the average rate of change within the range

`-7\le x\le-4`

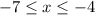
- These interval limits give us the values of x1, and x2.

- Thus, we simply need to find the corresponding values f(x1) and f(x2). This is done by reading off the graph.

- Reading off the graph, we have that:

`\begin{gathered} (x_1,f(x_1))=(-7,25) \\ \\ (x_2,f(x_2))=(-4,10) \end{gathered}`

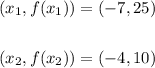
- Thus, we can proceed to calculate the average rate of change as follows:

`\begin{gathered} (\Delta y)/(\Delta x)=(f(x_2)-f(x_1))/(x_2-x_1) \\ \\ (\Delta y)/(\Delta x)=(10-25)/(-4-(-7))=-(15)/(-4+7) \\ \\ \therefore(\Delta y)/(\Delta x)=-(15)/(3)=-5 \end{gathered}`

Final Answer

The average rate of change is -5