Question

what are the length and width of a rectangle if tje length is 5meters longer than the width?the area is 126m^2.

Answer 1

We will begin solving the question by sketching the image to solve the question

Given:

The length of the rectangle is 5 meters longer than the width

The area of the rectangle is 126 square meters

This means that L=5+w

We will use the relationship:

`\text{Area}=\text{length}* width`
`\begin{gathered} \text{Area}=(w+5)w=126 \\ \text{simplifying} \\ w^2+5w=126 \\ w^2+5w-126=0 \end{gathered}`

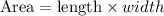
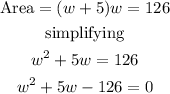
Simplifying further

`w^2+14w-9w-126=0`
`\begin{gathered} w(w+14)-9(w+14)=0 \\ (w+14)(w-9)=0 \end{gathered}`
`\begin{gathered} w=9 \\ or \\ w=-14 \end{gathered}`

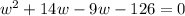
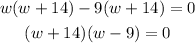
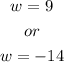
The width can only be positive

so that

width = 9 meters

so that the length will be w+9

Length = w+9 =9 +5 =15

Length =15 meters

Therefore

width = 9 meters

Length = 14 meters