Question

Emanuel wants to save $600 to buy a TV. He saves 18 each week. The amount A (in dollars) that he still needs after w weeks is given by the following function.A (w) = 600-18w

Answer 1

We have been given that the formula that defines the amount A (in dollars) that he still needs after w weeks is given by the following function.

`A(w)=600-18w`

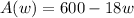
Part A

We are told to find how much money Manuel still needs after 7 weeks. To do this, we will simply substitute w=7

`\begin{gathered} A(7)=600-18*7 \\ A(7)=600-126 \\ A(7)=\text{ \$474} \end{gathered}`

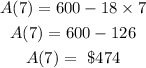
Emmanuel still needs to save $474

Part B

We are told to find the number of weeks Emanuel has been saving if he still needs $294.

To do this we will simply substitute A(w) =294 and solve for w.

So that

`294=600-18w`

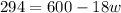
To solve this, we will collect like terms

`\begin{gathered} 18w=600-294 \\ 18w=306 \end{gathered}`

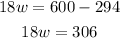
Dividing both sides by 18

`\begin{gathered} (18w)/(18)=(306)/(18) \\ \\ w=17 \end{gathered}`

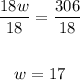
This means that Emmanuel has been saving for 17 weeks