Two lines are perpendicular between each other if their slopes fulfills the following property
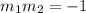
where m1 and m2 represents the slopes of line 1 an 2, respectively.
To find the slope of a line we can write it in the form slope-intercept form

Our original line is
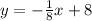
Then its slope is

Now we have to find the slope of the second line. Using the first property,
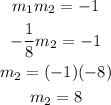
Then the second line has to have a slope of 8.
The options given to us are:

Then we have to determine which of these options have a slope of 8. To do that we write them in the slope-intercept form:
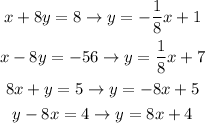
Once we have the options in the right form, we note that the only one of them that has a slope of 8 is the last one.
Then the line perpendicular to the original one is
