Question

Find the leading term degree and coefficient of the function f(x)=(x+1)(3x-1)(4x+1)^3

Answer 1

To find the leading term degree and coefficient we need to expand the function:

`\begin{gathered} f(x)=(x+1)(3x-1)(4x+1)^3 \\ =(3x^2-x+3x-1)((4x)^3+3(4x)^2(1)+3(4x)(1)^2+1^3) \\ =(3x^2+2x-1)(64x^3+3(16x^2)+12x+1) \\ =(3x^2+2x-1)(64x^3+48x^2+12x+1) \\ =192x^5+144x^{4^{}}+36x^3+3x^2+128x^4+96x^3+24x^2+2x-64x^3-48x^2-12x-1 \\ =192x^5+272x^4+68x^3-21x^2-10x-1 \end{gathered}`

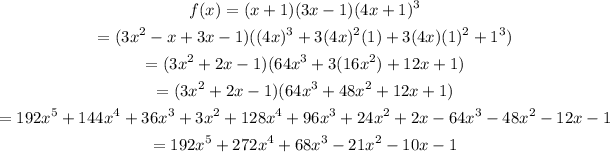
From this we conclude that the polynomial is of degree 5, that is the leading term has degree 5 and its coefficient is 192.

The graph of the function is:

From this we notice that:

The function increases in the intervals:

`\begin{gathered} (-\infty,-0.833) \\ \text{and} \\ (0.2,\infty) \end{gathered}`

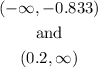
The function decreases in the interval:

`(-0.833,02)`

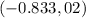
Furthermore as the variable tends to minus infinity the function also tends to minus infinity; whereas as the variable tends to infinity the function tends to inifnity, that is:

`\begin{gathered} \lim _(x\to-\infty)f(x)=-\infty \\ \lim _(x\to\infty)f(x)=\infty \end{gathered}`