Question

2. Find a polynomial function, p(2), of lowest degree, with zeros -4i and 2 (with multiplicity2). The answer should be a factored function.I am confused about the wording, how do I solve this? Do they want me to leave it in factored form? Or make an equation?

Answer 1

To determine a polynomial function p(2) of lowest degree:

If a polynomial function f(x) has the numbers a, b as zeros then (x-a) and (x-b) are all factors of f(x). Also complex roots occur in conjugate pairs so if 0 + 4i is a zero then 0 - 4i is also a zero. So a polynomial is

`\begin{gathered} f(x)=(x-2)(x-4i)(x+4i) \\ f(x)=(x-2)(x^2+4i-4i-16i) \\ f(x)=(x-2)(x^2-16i^2) \\ \text{where i}^2\text{ = -1} \\ f(x)=(x-2)(x^2-16(-1)) \\ f(x)=(x-2)(x^2+16) \end{gathered}`
`\begin{gathered} f(x)=x(x^2+16)-2(x^2+16) \\ f(x)=x^3+16x-2x^2-32 \\ f(x)=x^3-2x^2+16x-32 \end{gathered}`

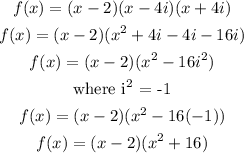
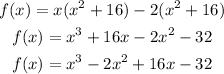
To check that the given numbers are all zeros of the polynomial :

`\begin{gathered} f(x)=x^3-2x^2+16x-32 \\ f(2)=2^3-2(2)^2+16(2)-32 \\ f(2)=8-8+32-32 \\ f(2)=0 \end{gathered}`

Therefore the factored function of the polynomial f(x) = x³-2x²+16x-32