Question

Consider the following exponential function.f(x) = 4" - 3As the value of x decreases, the value of f(x) approachesThe graph of function f crosses the y-axis at the pointThe graph of function f crosses the x-axis between the x-values of

Answer 1

When the values of x decreases, the value 4^x goes towards 0. So the function will have only the constant value -3, so as the value of x decreases, the value of f(x) approaches -3.

To find the crossing point with the y-axis, we just need to calculate the value of f(0), that is, the value of the function when x = 0. So we have:

`\begin{gathered} f(x)=4^x-3 \\ f(0)=4^0-3 \\ f(0)=1-3 \\ f(0)=-2 \end{gathered}`

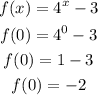
So the crossing point with the y-axis is (-2, 0).

To find the crossing point with the x-axis, we just need to calculate the value of x for f(x) = 0. So we have:

`\begin{gathered} f(x)=4^x-3 \\ 0=4^x-3 \\ 4^x=3 \\ \log (4^x)=\log (3) \\ x\cdot\log (4)=\log (3) \\ x=(\log(3))/(\log(4))=(0.47712)/(0.60206)=0.79248 \end{gathered}`

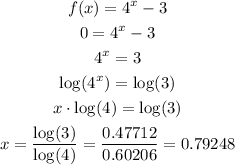
So this value of x is between 0 and 1.