Question

The population of a certain bacteria has an initial population of 375 cells and grows at a continuous growth rate of 1956 per minute: Write a continuous exponential model for this scenario and find the time, to the nearestwhole minute, it takes for the bacteria to double its population.Help solve B A) P(t)=375^0.19tB) It takes ____ minutes for the bacteria to double it’s population.

Answer 1

The model provided in the question is given to be:

`P(t)=375e^(0.19t)`

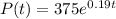
Double the bacteria population is:

`\Rightarrow375*2=750`

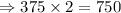
To find the time taken to get that population, we will equate P(t) to 750. Therefore,

`750=375e^(0.19t)`

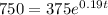
We can solve this using the following steps.

Step 1: Divide both sides by 375

`\begin{gathered} (750)/(375)=(375e^(0.19t))/(375) \\ 2=e^(0.19t) \\ \Rightarrow e^(0.19t)=2 \end{gathered}`

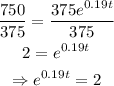
Step 2: Find the natural logarithm of both sides

`\ln e^(0.19t)=\ln 2`

Step 3: Recall that the product of the natural logarithm and the natural exponent is the same. Hence, we have

`0.19t=\ln 2`

Step 4: Divide both sides by 0.19

`\begin{gathered} (0.19t)/(0.19)=(\ln 2)/(0.19) \\ t=(\ln 2)/(0.19) \end{gathered}`

Step 5: Evaluate the answer using a calculator

`t=3.6\approx4`

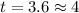
ANSWER

It takes 4 minutes for the bacteria to double its population.