Question

Suppose that the functions and g are defined as follows.f(x) = 5x+4g(x) = 4x + 1Find fg and / g. Then, give their domains using interval notation

Answer 1

Given that:

`\begin{gathered} f(x)\text{ = 5x + 4} \\ g(x)\text{ = }\sqrt[]{4x\text{ + 1}} \end{gathered}`

Solution

1. (f.g)(x)

`\begin{gathered} (fg)(x)\text{ = (5x + 4)(}\sqrt[]{4x+\text{ 1}}) \\ =\text{ 5x(}\sqrt[]{4x+1})\text{ + 4(}\sqrt[]{4x+\text{ 1}}) \end{gathered}`

The domain of f.g: The domain represents the values of x for which (f.g)(x) is defined

`\text{ Domain : \lbrack}0,\text{ }\infty\rbrack`

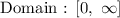
Answer:

f.g = 5x(sqrt(4x + 1) + 4(sqrt(4x + 1))

Domain : [0,positive infinity]

2. (f - g)(x)

`\begin{gathered} (f-g)(x)\text{ = 5x + 4 - (}\sqrt[]{4x+\text{ 1}}) \\ =\text{ 5x + 4 -}\sqrt[]{4x\text{ + 1}} \end{gathered}`

The domain of f-g:

`\text{Domain : \lbrack}0,\text{ }\infty\rbrack`

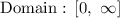
Answer:

f-g : 5x + 4 - sqrt(4x + 1)

Domain : [0, positive infinity]

N.B sqrt means square root