To answer this question, we have two situations in which we have two events that are used to decide a situation. In each case, we need to determine if the outcomes are equally likely.
Then we can proceed as follows:
First Situation
We have John and Martin, and it is about to decide who will be to bat first.
If we flip a coin to decide that, we know, from probability theory, that the probability to get a head is 0.50, and the probability of getting a tail is also 0.50. Therefore, this situation is statistically fair.
Second Situation
The results of a die are equally likely (if we have a fair die), and the outcomes are 1, 2, 3, 4, 5, and 6.
Then if we calculate the probability of having 1, 3, and 5, we have:
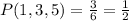
And if we calculate the probability of getting 2, 4, or 6 is also:
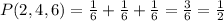
Then both events are equally likely to happen.
Therefore, in summary, we can say that the two situations are statistically fair.