Question

3. You are given a three-digit number. Reverse the digits of this number so that the units digit and the hundreds digit are interchanged. The product of your original three-digit number and your reversed number must equal 65125. What three-digit factor is the smaller of the two numbers?

Answer 1

We can express a three-digits number as

`100h+10t+u`

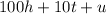
Where h represents hundreds, t represents tens, and u represents units.

Then, we change the units and hundreds to express the second number.

`100u+10t+h`

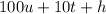
According to the problem, the product of these two numbers must be equal to 65,125.

`(100h+10t+u)(100u+10t+h)=65,125`

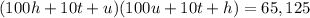
Let's multiply using the distributive property

`10,000hu+1000ht+100h^2+1000tu+100t^2+10ht+100u^2+10tu+hu=65,125`

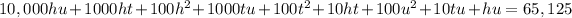
As you can observe, the last digit of the number is obtained by multiplying the hundreds (h) and the units (u). Given that the number ends in 5, the possibilities are 1, 3, 5, 7, or 9. Trying out these possibilities, the smallest number containing 3 is 305, its reversed number is 503, and their product is 153,415 which is not correct.

Trying the possibilities to look for the smallest number using each digit, we get 125, its reversed number is 521, their product is 65,125, which is the number given by the problem

Hence, the smallest three-digit factor is 125.