From the problem, we have :
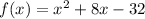
Set f(x) = 0 :
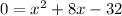
Add 32 to both sides of the equation :
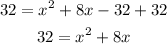
Next is to add a number to both sides of the equation using the formula (b/2a)^2
That will be :
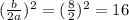
The equation will be :

Take note that the right side of the equation is now a perfect square trinomial and we can factor it by :
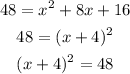
Take the square root of both sides :
![\begin{gathered} \sqrt[]{(x+4)^2}=\sqrt[]{48} \\ x+4=\pm4\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2ge7ltn0x2eax9glkuqpxixcocsvpws7t4.png)
Subtract 4 to both sides of the equation :
![\begin{gathered} x+4-4=-4\pm4\sqrt[]{3} \\ x=-4\pm4\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6tcei0678ajukrnxgxr2l9jhznoy997sex.png)
Take note that zeros and x-intercepts are the same.
Therefore, the answer is :
A. The zeros and the x-intercepts are the same. They are -4 + 4√3 and -4 - 4√3