Answer:
B. The zeros are -2/3 and -3 because y=(3x+2)(x+3)
Step-by-step explanation:
Given the equation:
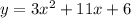
To find the zeros, first, factorize the expression:
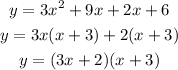
Next, set the factored expression equal to 0.
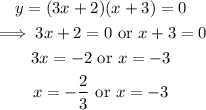
Thus, the zeros are -2/3 and -3 because y=(3x+2)(x+3).
The correct choice is B.