Question

Discriminant for x^2-4x+1=-3

Answer 1

The given equation is

`x^2-4x+1=-3`

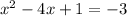
First, we have to move the term -3

`\begin{gathered} x^2-4x+1+3=0 \\ x^2-4x+4=0 \end{gathered}`

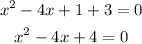
Where a = 1, b = -4, and c = 4.

The discriminant formula is

`D=b^2-4ac`

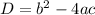
Replacing the values, we have

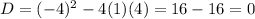
`D=(-4)^2-4(1)(4)=16-16=0`The discriminant is zero.

Given that the discriminant is zero, it means the equation has a unique solution.