Question

The box shown on the rough ramp above is sliding up the ramp.calculate the force of friction on the box

Answer 1

We are given a box that slides up a ramp. To determine the force of friction we will use the following relationship:

`F_f=\mu N`

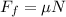
Where.

`\begin{gathered} N=\text{ normal force} \\ \mu=\text{ coefficient of friction} \end{gathered}`

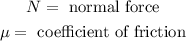
To determine the Normal force we will add the forces in the direction perpendicular to the ramp, we will call this direction the y-direction as shown in the following diagram:

In the diagram we have:

`\begin{gathered} m=\text{ mass}_{} \\ g=\text{ acceleration of gravity} \\ mg=\text{ weight} \\ mg_y=y-\text{component of the weight. } \end{gathered}`

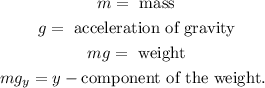
Adding the forces in the y-direction we get:

`\Sigma F_y=N-mg_y`

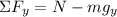
Since there is no movement in the y-direction the sum of forces must be equal to zero:

`N-mg_y=0`

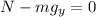
Now we solve for the normal force:

`N=mg_y`

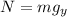
To determine the y-component of the weight we will use the trigonometric function cosine:

`\cos 40=(mg_y)/(mg)`

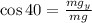
Now we multiply both sides by "mg":

`mg\cos 40=mg_y`

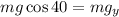
Now we substitute this value in the expression for the normal force:

`N=mg\cos 40`

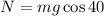
Now we substitute this in the expression for the friction force:

`F_f=\mu mg\cos 40`

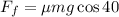
Now we substitute the given values:

Solving the operations:

`F_f=15.01N`

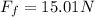
Therefore, the force of friction is 15.01 Newtons.