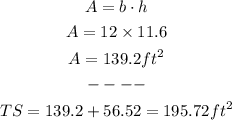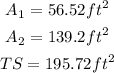
1) In this picture, we can discern a trapezoid, a triangle, and one semicircle.
2) Let's begin from top to bottom, figuring out the area of that semicircle. A semicircle is half the area of a circle, so we can write out the following formula:
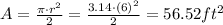
Note that the diameter of that semicircle is congruent to the side of the parallelogram. And the diameter is twice the radius, so the radius is 6 ft long.
As we were told, we're considering an approximation for the value of pi.
3) Now, let's move on to the parallelogram. The area of a Parallelogram is