Given the coordinates for the function:
Gallons of gas Cost, in Dollars
1 1.25
2 2.50
5 6.25
15 18.25
25 25.00
Let's find the coorddinates of the inverse.
To find the coordinats of the inverse, let's find the original function.
Apply the slope-intercept form of a linear function:
y = mx + b
Where m is the rate of change and b is the y-intercept.
To find the rate of change, we have:
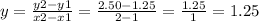
To solve for b, we have:

The function for the given table is:
y = 1.25x
To find the inverse of the function, let's interchange the variables:
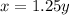
Solve for y:
Divide both sides by 1.25

Therefore, the inverse of the function is:
y = 0.8x
Let's find the coordinates of the inverse function.
When x = 1:
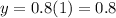
When x = 2:
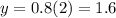
When x = 3:
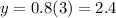
When x = 4:

When x = 5:
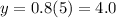
Therefore, the coordinates for the inverse function are:
Gallons of Gas Cost in dollars
1 0.8
2 1.6
3 2.4
4 3.2
5 4.0
ANSWER:
Gallons of Gas Cost in dollars
1 0.8
2 1.6
3 2.4
4 3.2
5 4.0