Question

Find the standard deviation ofthe given data rounded to thenearest hundredth.12, 53, 141, 219, 500

Answer 1

`173.014`

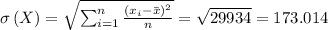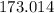
1) Let's find the standard deviation for this data set:

`12,53,141,219,500`

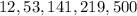
2) So, let's apply the formula for standard deviation:

`\begin{gathered} S\left(X\right)=\sqrt{\frac{\sum_(i=1)^n\left(x_i-\bar{x}\right)^2}{n}} \\ \end{gathered}`

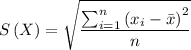
3) Let's find the mean and compute the variance:

`\bar{x}=\sum_(i=1)^na_i=(12+53+141+219+500)/(5)=(925)/(5)=185`

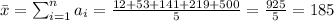
The sum of all entries is divided by the number of data points.

Now, for the variance:

`\begin{gathered} \sum_(i=1)^n\left(x_i-\bar{x}\right)^2=(\left(12-185\right)^2+\left(53-185\right)^2+\left(141-185\right)^2+\left(219-185\right)^2+\left(500-185\right)^2)/(5) \\ (149670)/(5)=29934 \end{gathered}`

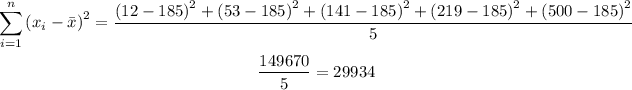
Finally, we can take the square root of that variance to get the standard deviation:

`\sigma\left(X\right)=\sqrt{\sum_(i=1)^n\frac{\left(x_i-\bar{x}\right)^2}{n}}=√(29934)=173.014`