Equality
In this case, we'll have to carry out several steps to find the solution.
Step 01:
Data
sec θ - sinθ tanθ = cos θ
prove the identity = ?
Step 02:
We must use the trigonometric identities to find the solution.
sec θ - sinθ tanθ = cos θ
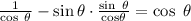
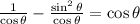
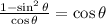
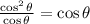
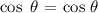
The answer is:
Equality is verified.
cos θ = cos θ