Given in the question:
a.) One aquarium contains 2.1 cubic feet of water.
b.) The other aquarium contains 1.4 cubic feet of water.
c.) The water in the larger aquarium weighs 43.68 pounds more than the water in the smaller aquarium.
To be able to answer this type of problem, we will be applying the ratio and proportion:
We get,

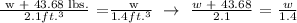
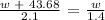
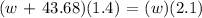
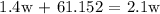
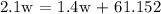
Therefore, the equation is 2.1w = 1.4w + 61.152
Let's determine the value of w:
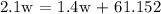
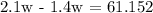
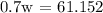
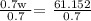
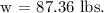
Let's determine the weight of 1 cubic foot of water:
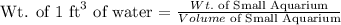
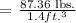
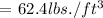
Therefore, the weight of 1 cubic foot of water is 62.4 lbs.