Question

Government limits for sea water are based on an iodine 131 value of 40 Bq/L and a cesium 137 value of 90 Bq/L. On April 17, 2011, sea water contamination levels based on samples 20 km from the site had iodine 131 and cesium 137 concentrations of 161 Bq/L and 186 Bq/L, respectively. How much time must pass before the sea water sample reaches the government's limits?

Answer 1

we know the equation of radiactive decreasing is:

`m_f=m_ie^(-\lambda t)`

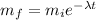
where mf is the final concentration (40 and 90 bq/L) mi is the initial concentration (161 and 186 bq/L), lamda is the decreacion constant of each element and t is the time, so we replace the information and solve the equation for t:

`\begin{gathered} \ln ((m_f)/(m_i))=-\lambda t \\ \lambda(\ln (m_i)-\ln (m_f))=t \end{gathered}`

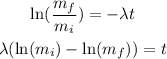
So if lamda is equal to 20 we replace:

`\begin{gathered} 20\ln ((161)/(40))=t \\ 20\cdot1.4=t \\ 28=t \end{gathered}`

Si they have to wait 28 years