Question

I need these answers with 100% accuracy look at the screenshots

Answer 1

In order to determine the values of x and y, proceed as follow:

- Consider that the bigger and smaller triangle are similar, then, they have similar sides in which thier proportion are equal. Based on the given image you can write:

`(28)/(y)=(y)/(8)`

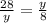
By solving for y, you get:

`\begin{gathered} y^2=28*8 \\ y=\sqrt[\placeholder{⬚}]{224} \\ y=4\sqrt[\placeholder{⬚}]{14} \end{gathered}`

- Now, use the Pythagorean theorem to find the value of x:

`\begin{gathered} 28^2=x^2+y^2 \\ x^2=28^2-y^2 \\ x=\sqrt[\placeholder{⬚}]{28^2-(4\sqrt[\placeholder{⬚}]{14})^2} \\ x=4\sqrt[\placeholder{⬚}]{35} \end{gathered}`

Hence, the values of x and y are:

x = 4√35

y = 4√14

Fourth option