Question

8x^ +7x + 1 = 0Round your answer to the nearest hundredth.

Answer 1

Quadratic Equations

The general form of a quadratic equation is:

`ax^2+bx+c=0`

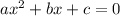
Where a, b, and c are constants.

We can solve the quadratic equation by using the following formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

The equation:

`8x^2+7x+1=0`

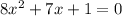
Has the coefficients a = 8, b = 7, c = 1. Substituting:

`x=\frac{-7\pm\sqrt[]{7^2-4\cdot8\cdot1}}{2\cdot8}`

Operating:

`\begin{gathered} x=\frac{-7\pm\sqrt[]{49-32}}{16} \\ x=\frac{-7\pm\sqrt[]{17}}{16} \end{gathered}`

There are two real solutions:

`\begin{gathered} x_1=\frac{-7+\sqrt[]{17}}{16} \\ x_2=\frac{-7-\sqrt[]{17}}{16} \end{gathered}`

Calculating:

x1 = -0.18

x2 = -0.70