Question

Using only the Descartes' Rule of signs, determine the possible number of NEGATIVE zeros when f(x)=x5 - 3x3 + 2x2 + 5x - 4.

Answer 1

0 or 2. Option A is correct

Explanations:

Given the polynomial function expressed as:

`x^5-3x^3+2x^2+5x-4`

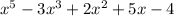
According to the Descartes' Rule, the number of positive real zeros in a polynomial function f(x) is the same or less than by an even numbers as the number of changes in the sign of the coefficients.

In order determine the possible number of negative zeros, we will first determine the number of times the sign of the coefficient of each term changes

This shows that the sign changes 2 times as shown above. Subtracting 2 from the total number of times the sign changes will give 2 - 2 = 0.

Hence the possible number of NEGATIVE zeros is 0 or 2