Hello!
First, let's analyze the exercise and get some important information:
• The kayaker’s speed while ,traveling upstream, is 4 miles per hour.
,
• His speed ,going downstream, is 7 miles per hour.
Let's write it as a system with variables:
• k ,= speed of the kayaker
,
• c, = speed of the current
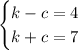
If we add these two equations, we can cancel C, look:
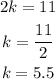
Now that we know the value of k, let's replace it in the first equation:
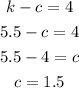
What is the kayaker speed still in the water? 5.5mi/h
What is the speed of the current? 1.5mi/h