Question

Graph the expression on each side of the equals symbol to determine wether the equation might be an identity:

Answer 1

The graph of the left side of the equation is shown below:

The graph of the right side of the equation is shown below:

Comparing them we notice that they are the same graph, therefore the equation is an identiy.

To prove the idenity we need to remember that:

`\begin{gathered} \csc \theta=(1)/(\sin \theta) \\ \cot \theta=(\cos \theta)/(\sin \theta) \end{gathered}`

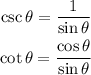
also, we need to remember that:

`1-\cos ^2\theta=\sin ^2\theta`

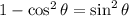
Let's use this properties on the left side of the equation:

`\begin{gathered} (\csc \theta+\cot \theta)(1-\cos \theta)=((1)/(\sin\theta)+(\cos\theta)/(\sin\theta))(1-\cos \theta) \\ =(\frac{1+\cos \theta}{\sin ^{}\theta})(1-\cos \theta) \\ =((1+\cos \theta)(1-\cos \theta))/(\sin \theta) \\ =\frac{1-\cos ^2\theta}{\sin ^{}\theta} \\ =(\sin ^2\theta)/(\sin \theta) \\ =\sin \theta \end{gathered}`

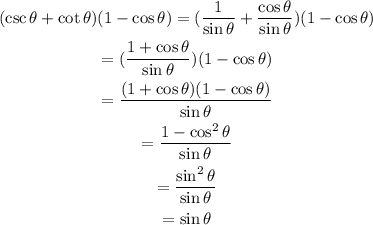
Therefore:

`(\csc \theta+\cot \theta)(1-\cos \theta)=\sin \theta`

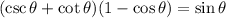
and we proved what we noticed on the graphs.