ANSWER:
191.5 feet
Explanation:
According to the statement, we can plan the following graph that represents the situation:
We can see two right triangles in the figure graph ABC and DBC. Where the width of the river would be x.
We can calculate the value of x with the help of the tangent trigonometric ratio, just like that.

We match both equations so that you can calculate the value of x:
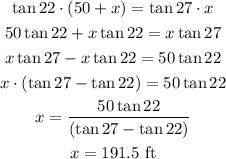
Therefore, the wide of the river is 191.5 feet.