Question

Determine whether the following infinite geometric series diverges or converges. If the series converges, state the sum.8 + 32 + 128+ • • •

Answer 1

A geometric series is given by

`\sum ^(\infty)_(n\mathop=0)a_1(r)^(n-1)`

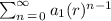
Where a1 represents the first term and r represents the common ratio.

The first term of our series is 8, and to find the common ratio we just need to divide one term by the previous one.

`(32)/(8)=4`

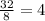
Our geometric series is

`\sum ^(\infty)_{n\mathop{=}0}8(4)^(n-1)`

A geometric series converges if and only if

[tex]-1the common ratio is within this range. Since 4 is not on this range, this series diverges.