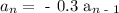Question

Write a recursive formula for the following sequence. If your answer is not an integer type it as a decimal rounded to the nearest tenth.a_n = {10,-3,0.9,-0.27,...}a_n = Answer*a_{n-1}

Answer 1

Consider the following set:

`a_n=\lbrace10,\text{ -3, 0.9, -0.27}\rbrace`

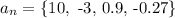
This type of sequence represents a Geometric sequence in which the ratio between any two consecutive terms is constant.

Now, to know that it is actually a geometric sequence, divide each term in a sequence by the preceding term. If the resulting quotients are equal, then the sequence is geometric.

According to the definition of a geometric sequence, we have that a recursive formula for the given sequence would be

`a_1=10`
`a_n=\text{ - 0.3 a}_{n\text{ - 1}}`

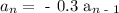
Then, we can conclude that the correct answer is:

`a_n=\text{ - 0.3 a}_{n\text{ - 1}}`