Question

When Peyton left her house in the morning, her cell phone battery was partially charged. Let BB represent the charge remaining in Peyton's battery, as a percentage, tt hours since Peyton left her house. The table below has select values showing the linear relationship between tt and B.B. Determine how many hours after leaving her house it would take until the phone's battery level got down to 24.75%.

Answer 1

Given the table:

t B

1 22.5

3 13.5

5.5 2.25

Where B represents the charge remaining in Peyton's battery.

And t represents the number of hours since Peyton left her house.

Let's determine the number of hours it would take until the phine's battery level get down to 24.75%.

First of all, let's create a linear equation that is represented on the table.

Apply the slope intercept form of a linear equation:

y = mx + b

Where m is the slope.

To find the slope apply the slope formula:

`m=(y2-y1)/(x2-x1)`

Take two points on the table:

(x1, y1) ==> (1, 22.5)

(x2, y2) ==> (3, 13.5)

Thus, we have:

`\begin{gathered} m=(13.5-22.5)/(3-1) \\ \\ m=(-9)/(2) \\ \\ m=-4.5 \end{gathered}`

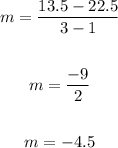
To solve for b, susbtitute -4.5 for m, and input one of the points for the values of x and y:

`\begin{gathered} y=mx+b \\ \\ 22.5=-4.5(1)+b \\ \\ 22.5=-4.5+b \\ \\ \text{Add 4.5 to both sides:} \\ 22.5+4.5=-4.5+4.5+b \\ \\ 27=b \\ \\ b=27 \end{gathered}`

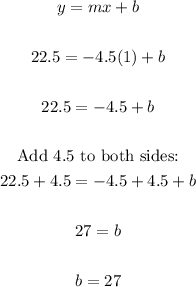
Therefore, the equation that represents this situation is:

y = -4.5x + 27

To find the number of hours it would take until the phone's battery level got down to 24.75%, substitute 24.75 for y in the equation and solve for x.

y = -4.5x + 27

24.75 = -4.5x + 27

Subtract 27 from both sides:

24.75 - 27 = -4.5x + 27 - 27

-2.25 = -4.5x

Divide both sides by -4.5:

`\begin{gathered} (-2.25)/(-4.5)=(-4.5x)/(-4.5) \\ \\ 0.5=x \end{gathered}`

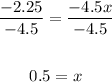
Therefore, it would take 0.5 hour for the phone's battery level to get down to 24.75%.

ANSWER:

0.5