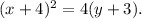Question

Convery the equation of the parabola to standard form. Show all work.

Answer 1

Recall that the equation of a vertical parabola in standard form is as follows:

`\mleft(x-h\mright)^2=a\mleft(y-k\mright),`

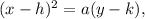
where (h,k) is the vertex of the parabola.

Adding 4y-4 to the given equation we get:

`\begin{gathered} x^2+8x-4y+4+4y-4=0+4y-4,^{} \\ x^2+8x=4y-4. \end{gathered}`

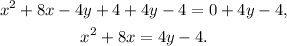
Adding 16 to the above equation we get:

`\begin{gathered} x^2+8x+16=4y-4+16, \\ x^2+8x+16=4y+12. \end{gathered}`

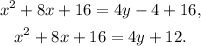
Now, notice that:

`\begin{gathered} x^2+8x+16=x^2+2\cdot4\cdot x+4^2=(x+4)^2, \\ 4y+12=4(y+3). \end{gathered}`

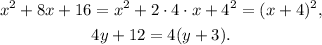
Therefore we can rewrite the given equation as follows:

`(x+4)^2=4(y+3)\text{.}`

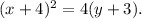
Answer:

`(x+4)^2=4(y+3)\text{.}`