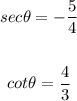Given:
Given θ is an angle in Quadrant III.
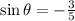
Required:
To find the value of secθ and cotθ.
Step-by-step explanation:
In Quadrant III, cosine (the x-value of the unit circle) and sine (the y-value of the unit circle) are both negative and tangent is positive.
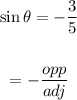
To find the adjacent side of the triangle use the Pythagorean Theorem:
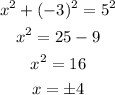
Since we are in the third quadrant
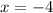
One way to find the secant and cotangent is to use the inverse identities:
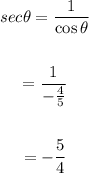
And
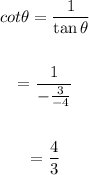
Final Answer: